| H1
¤¤
Harry
discutait ce jour là avec le jeune fils de son voisin,
lequel venait de se faire construire une piscine rectangulaire.
Il lui demanda quelles en étaient les dimensions.
Le garçon répondit :
"Je
sais seulement que les dimensions en mètres sont
des nombres sans virgule, et que l'aire en m² est égale
au périmètre en mètres".Harry
réfléchit, et dit : "Est-ce que
ta piscine est carrée ?". Et le garçon
répondit par la négative. Quelles sont
les dimensions de la piscine ?
|
H2
¤¤¤¤
D'après
son réveil à affichage digital, il était
juste l'heure pour Harry d'aller à son rendez-vous.
Mais, ébloui par le soleil hivernal, il ne s'aperçut
pas qu'il ne voyait pas directement le réveil, mais
uniquement son reflet dans un miroir, et il arriva au rendez-vous
avec 20 minutes d'avance. L'affichage du réveil était
de la forme :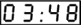
et
les chiffres possibles sont: 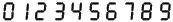
Quelle heure était-il réellement lorsqu'il
a regardé le réveil ?
|
H3
¤¤
A
l'occasion de l'anniversaire de sa femme, le roi du Mathématistan
a décidé de lancer une nouvelle collection
de 6 pièces de monnaie .La plus grosse des pièces
aura pour valeur l'âge de sa tendre épouse;
chaque pièce aura pour valeur un des diviseurs possibles
de cet âge (il y aura autant de pièces que
de diviseurs), et, délicatesse supplémentaire,
la plus grosse des pièces aura autant de valeur que
toutes les autres réunies... Quel est l'âge
de la reine du Mathématistan ?!
|
| H4
¤¤
On
a interrogé 100 garçons d'un collège.
Parmi eux, 65 possédaient chez eux une Playstation
(one ou 2), 46 avaient une Dreamcast et 90 une GameBoy (classique,
Pocket, Color ou Advance)...Combien de garçons
au minimum possédaient à la fois les trois
types de consoles ?
|
H5
¤¤¤¤
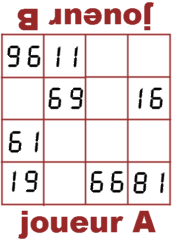 |
Ce
carré magique a une curieuse propriété
: Quand on le retourne, et qu'on se place dans la
position du joueur B, pour peu qu'on écrive
les chiffres de la façon suivante :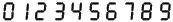 ,
on obtient un deuxième carré magique,
différent, mais qui a la même "somme
magique" que le premier ! (On rappelle que, dans
un carré magique, la somme des nombres d'une
ligne, d'une colonne ou d'une diagonale donne toujours
le même résultat, qui s'appelle la "somme
magique" du carré). Vous en savez assez
pour le compléter ! ,
on obtient un deuxième carré magique,
différent, mais qui a la même "somme
magique" que le premier ! (On rappelle que, dans
un carré magique, la somme des nombres d'une
ligne, d'une colonne ou d'une diagonale donne toujours
le même résultat, qui s'appelle la "somme
magique" du carré). Vous en savez assez
pour le compléter !
|
|
| H6
¤
Une
énorme comète se dirige directement vers la
terre ! Il y a deux jours, elle en était à
1 000 000 de km, hier à 100 000 km;
aujourd'hui, elle n'en est plus qu'à 10 000
km et les astronomes ont calculé que demain, il ne
lui resterait plus que 1 000 km à parcourir
avant de s'écraser sur notre planète ! En
supposant que la comète poursuive sa route exactement
à ce rythme, dans cette direction et ne rencontre
pas d'obstacle, combien de temps reste-t-il avant qu'elle
s'écrase sur la terre ?
|
H7
¤¤
Deux
frères, sont assis face à face à la
terrasse d'un café. Cela ne leur arrive pas très
souvent car ils habitent deux villes fort distantes. En
fait, ils ont pris l'habitude de se retrouver lorsque leurs
montres respectives indiquent la même heure... Ce
n'est curieux qu'en apparence, car il faut savoir que l'une
des montres avance de 17 minutes par jour, et l'autre retarde
de 7 minutes par 24 heures. Si l'on sait que ce sont deux
cadrans à aiguilles, et que, volontairement, aucun
des deux frères ne remet jamais sa montre à
l'heure, dans combien de temps se rencontreront-ils à
nouveau ?
|
H8
¤¤
Pouvez
vous trouver une figure, ou un objet quelconque, qui ait
à la fois un centre de symétrie et un nombre
impair, mais pas infini, d'axes de symétrie ?
|
| H9
¤¤
Sachant
qu'il faut 1 cl de peinture pour peindre une face d'un des
petits cubes, combien faudra-t-il de peinture pour repeindre
la totalité de cet objet, y-compris les faces sur
lesquelles il est posé ?
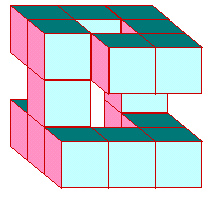
|
H10
¤¤
Comme
beaucoup de savants, le professeur Sacha Mnezik est très
distrait. Il a acheté un coffre-fort pour y loger
les résultats de ses dernières recherches,
lequel coffre-fort est doté d'une combinaison à
douze chiffres. Mais, n'ayant aucune confiance en sa mémoire,
il a pris soin de choisir une combinaison logique, qu'il
peut aisément retrouver avec un minimum de réflexion.
Les onze premiers chiffres sont :
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
|
1
|
2
|
2
|
3
|
2
|
4
|
2
|
4
|
3
|
4
|
2
|
Quel est le douzième
chiffre ?
|
H11
¤¤
Une
imprimerie doit envoyer 2002 calendriers à des clients
. Elle a donc confectionné des colis contenant chacun
le même nombre de calendriers ; en a rempli des
caisses contenant chacune le même nombre de colis,
et a expédié ces caisses par camion, chaque
camion contenant le même nombre de caisses. Il y a
286 calendriers par caisse, et 182 colis par camion.
Pouvez
vous trouver combien il y a de camions, de caisses dans
chaque camion, de colis dans chaque caisse et de calendriers
dans chaque colis ?
|
|

