Enigme N° 92
Retrouvez toutes les autres énigmes !

Communication d'entreprise...

Francis, le "Big Boss", a mis en place dans son entreprise 8 lignes téléphoniques directes entre certaines de ses 5 secrétaires. Zaza a une ligne directe avec Bibi, Annie, Dorothée et Charlotte. Bibi a aussi une ligne directe avec Dorothée et Charlotte.
Quant à Charlotte, elle a de plus une ligne directe avec Dorothée et Lulu.

Cela fait six secrétaires, direz-vous ! En effet ! Car l'une d'entre elles a été nommée ci-dessus par son vrai prénom, mais aussi par le surnom que lui donne Francis dans l'intimité...
Or, cet après-midi, pour tester ces nouvelles lignes téléphoniques, Francis a effectué l'opération suivante : il a donné une information à l'une de ses secrétaires. Celle-ci, en utilisant exclusivement une des lignes directes, devait transmettre l'information à une autre (et une seule), et ainsi de suite. A la fin, même si certaines secrétaires avaient reçu plusieurs fois l'information, toutes l'avaient entendue, et chacune des lignes directes avait été utilisée une et une seule fois.

Mais quel est le prénom et le surnom de la favorite de Francis ?

P.S : bien sûr, il n'y a pas deux lignes directes entre deux mêmes personnes,
ni une ligne entre une personne et elle-même !

 

Si vous connaissez une énigme amusante ou originale, n'hésitez pas à nous la proposer avec la solution et le nom de l'auteur (si vous le connaissez ; si c'est vous, c'est encore mieux !).
Nous nous ferons un plaisir de la publier dans les semaines à venir !

Proposer une énigme

 

Page d'accueil de Maths à Harry

 

Bravo à Mister Olive, Stiopa, Benjamin Fays, Evariste, Zarkan, Athos, Le Dgi, Eärendil, Matifouk et Nicolas Havet, qui sont les premiers à avoir trouvé qui était la favorite de Francis !

Le seul cas possible est qu'Annie soit Lulu...

On peut résoudre ce problème par élimination de façon très simple en remarquant que la seule personne qui n'a pas de ligne directe avec Charlotte est Annie. Or Charlotte a une ligne directe avec Lulu, et il n'y a pas deux lignes directes entre deux mêmes personnes.

Mais ce problème était aussi bien sûr une application du théorème d'Euler expliqué ci-dessous :

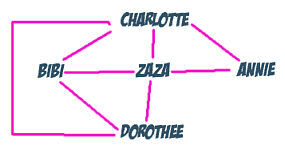
Ceci est un graphe.
Ce graphe comporte 5 sommets (A, B, C, D et Z).
Il comporte 8 arêtes (tous les " chemins " reliant deux sommets).
On nomme degré d'un sommet le nombre d'arêtes dont
ce sommet est une extrémité.
Ici, degré(A)=2; degré(B)=3; degré(C)=4;
degré(D)=3 ; degré(Z)=4.

En simplifiant, le théorème d'Euler dit deux chose :

1) Si tous les sommets sont reliés à un nombre pair (et différent de zéro) d'autres sommets, alors on peut partir de n'importe quel sommet et y revenir en ayant parcouru une et une fois chaque arête.

Dans le graphe ci-dessus, c'est impossible car B et D sont reliés à un nombre impair de sommets.

2) Sinon, si deux sommets exactement sont reliés à un nombre impair de sommets (les autres étant reliés à un nombre pair et non nul de sommets), on peut partir d'un de ces sommets et atteindre l'autre en ayant parcouru une et une fois toutes les arêtes.(Par contre, dans ce cas, on ne peut pas partir d'un point et revenir à son point de départ...)

Dans le graphe ci-dessus, il y a deux points exactement (B et D) qui sont reliés à un nombre impair de sommets. Donc on peut partir de B et aller jusqu'à D (ou aller de B jusqu'à D) en ayant parcouru une et une fois toutes les arêtes. Si on essaie de partir de n'importe quel autre point, c'est par contre impossible.

En partant de B (ou de D), il y a plusieurs possibilités... Par exemple :

BCZACDZBD

Pour conclure, on pourrait montrer (en essayant tous les cas) que si Annie n'était pas Lulu (donc si Charlotte n'avait pas de ligne directe avec Annie, mais en avait une autre avec n'importe quelle autre des secrétaires), non seulement les sommets ne pourraient pas être tous reliés à un nombre pair d'autres sommets, mais on n'aurait jamais deux sommets exactement reliés à un nombre impair de sommets.

Le théorème d'Euler ne s'appliquerait donc pas, et on ne pourrait pas passer une et une seule fois par chacune des arêtes...